HHL Portfolio Optimization, Round 1

Wealth doesn't grow under a mattress nor at the back of a dragon's cave.

¹

The Quantum Dragon is wise enough to know that he shouldn’t hoard treasure in his cave. Sure, it provides him with tangible assets, long-term wealth preservation, and a hedge against inflation, but it also subjects him to market volatility, poses security and logistical challenges, and provides no passive income whatsoever. He knows that investing in stocks historically leads to higher returns over the long term, which is important when your longevity is measured in centuries, and that dividends can provide an income stream that can be more reliable than village tributes. He further knows that he needs to diversify a stock portfolio in order to maximize opportunities while managing risk.

Of course, the only way The Quantum Dragon is willing to optimize his portfolio is with quantum computation. He’s not The Classical Dragon, people. And, of course, he has no interest whatsoever in dead-end algorithms. So, to have at least a little hope of realizing a computational advantage, he decided to take the Harrow, Hassidim, and Lloyd (HHL) algorithm out for a test flight. If you’re not familiar with it, the HHL algorithm proposes a potential exponential speedup for solving certain systems of linear equations. Unfortunately, it can’t be run on today’s noisy hardware, so he’ll have to settle for classical emulation for now. Still, proofs of concept are important.

The Benchmark Algorithm

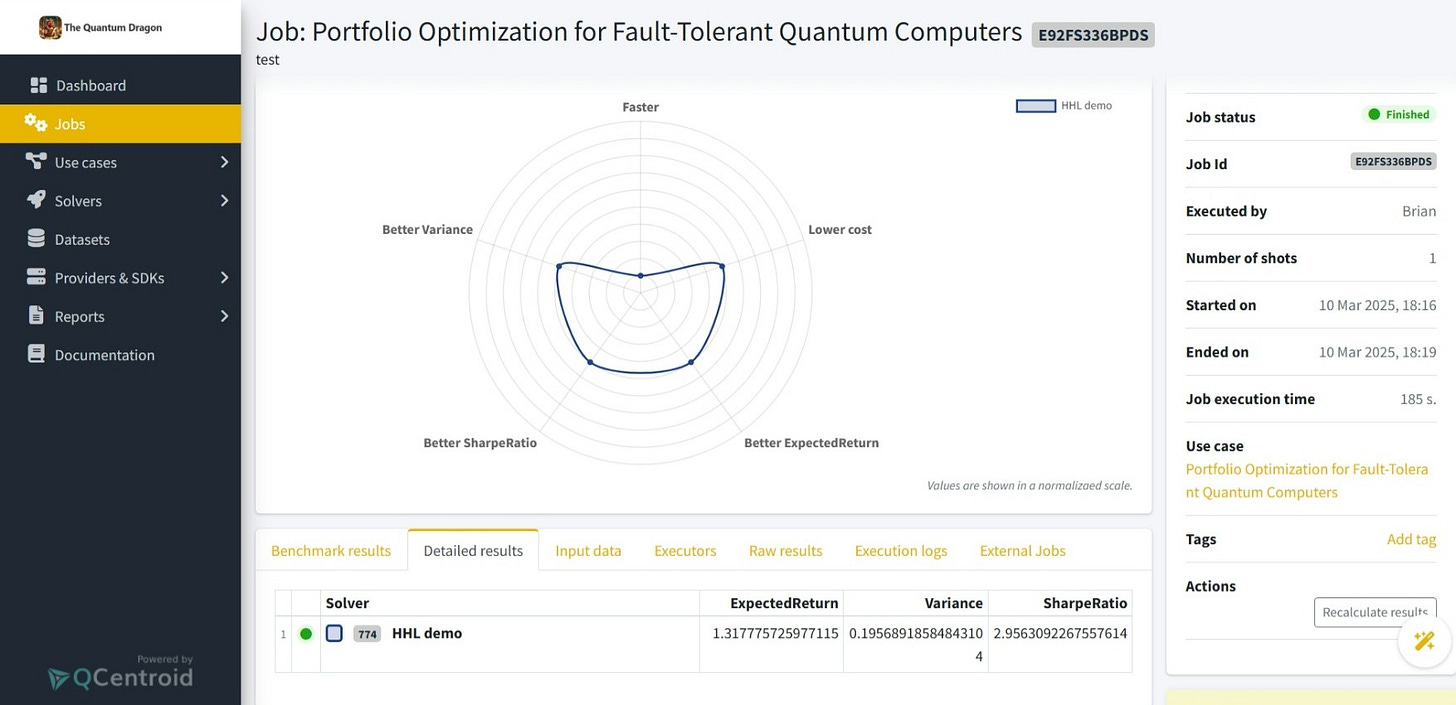
The first step, which he successfully accomplished, was simply to get it to work. He found some sample code on the internet which, of course, didn’t work at all, so he rebuilt it from scratch. It’s a simple mean-variance approach with two basic constraints: no short selling, and the sum of the allocations should equal 1.0. His initial objective wasn’t to impress anyone with this elementary framework, but rather to demonstrate that constraints can be implemented with an algorithm that has a potential exponential speedup. Now that he’s got the basics down pat, a future step will obviously be to implement a more practical, real-world framework.

NOTE: QCentroid lets you easily compare multiple solvers and/or hardware platforms, but this plot only shows that this first solver is working. Future articles will include other quantum and classical solvers on this plot so that the ease of making comparisons will become apparent.

Quantum vs. Classical

Despite his name, The Quantum Dragon has in fact dabbled with classical solvers before. His initial observation is that these classical solvers often have an objective function at their respective cores. Without getting too technical, the objective functions have a quadratic part to minimize variance and a linear part to minimize negative expected returns, which has the effect of maximizing expected returns. These solvers seem to focus on the quadratic terms, however, which minimizes variance so well that expected returns and other metrics are often quite low. The initial results from the HHL algorithm show higher variances, but with much more interesting expected returns and other metrics.

Logarithmic Scaling

One of the insights derived from building from scratch is that there is logarithmic scaling of the state register. A toy problem with only 4 stocks needs 2 qubits, while the S&P 500 needs only 9 and the Russell 2000 needs only 11. The circuit is still way, way too deep for today’s hardware, but it’s actually not that wide. This means that a moderate-sized problem — because we also have the counting and ancilla registers — can be classically emulated on most laptops. The technological challenge is actually building the quantum circuit, which easily crashes RAM using the selected SDK. One solution to this might be to not use a laptop, but a better solution is to use a more efficient SDK. Fortunately, there are quite a few out there to test.

Benchmarking with QCentroid

One way to find the most efficient SDK is to use the QCentroid platform. Once the algorithm has been ported to multiple SDKs, the solvers can all be run simultaneously. They can easily be compared on multiple benchmarks, including speed, RAM usage, and so forth. They can also be simultaneously compared to various classical solvers in regard to benchmarks such as expected returns, variances, and Sharpe ratios. The Quantum Dragon has partnered with QCentroid in large part due to the parallel execution of solvers, but honestly, he really loves the visualization that the platform returns. It is a remarkably intuitive way to compare multiple solvers.

Conclusion

This is the first article in a series. Maybe this will lead to a paper someday with the QCentroid team; wouldn’t that be exciting? But as this article has noted, there are many potential future steps ahead. There are SDKs to port to and classical solvers to upload. Once we’ve found the best SDK, we’ll need to add more constraints and make the approach more valuable. I don’t know if you’ve ever chatted with a dragon before about his treasure, but the notion of liquidating some of it to invest in stocks is serious business. The initial numbers are really exciting, but The Quantum Dragon knows enough people in finance to know that we want to minimize variance for important reasons. Do YOU want to tell him that he lost money? No, you do not.

1. Image generated by an AI model provided by Microsoft Copilot.